728x90

역행렬까진 쉽죠...기저 차원이 얼탈뿐...
#6. 역행렬
역행렬의 개념
행렬 A의 역행렬 B는 AB = I를 만족한다. 즉 행렬곱한 결과가 단위 행렬I가 되는 것을 의미한다.
단 역행렬을 구하고자 하는 행렬의 행렬식이 0일 경우 역행렬은 존재하지 않음
- 가역행렬 : 역행렬이 존재(유일), 행렬식 !=0
- 특이행렬 : 역행렬이 없음, 행렬식 = 0
역행렬 계산
2*2일때
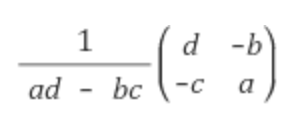
A = [[a,b],[c,d]]일때,
먼저 행렬식 !=0확인한 다음 좌측과 같이 계산
n*n일때
1. 각 원소 별 여인수(Cij)를 구함
2. 여인수로 이뤄진 여인수 행렬을 구함
3. 여인수 행렬의 전치행렬(transpose)인 행렬 A의 수반행렬(adj)을 구함
3. 행렬식을 구한 다음 (1/det(A)) * adj(A)로 역행렬 계산
정사각 행렬의 거듭 제곱
- A**0 = I
- An*Am = A(n+m)
- (An)m = Anm
역행렬의 성질
- 역행렬의 거듭제곱
- A**-n = (A**-1)**n
- 역행렬과 전치행렬
- (A**-1)**T = (A**T)**-1
- 역행렬과 행렬식
- det(A**-1) = 1/det(A). 즉 A의 역행렬의 행렬식은 A행렬식의 역수
파이썬 실습
#1. 넘파이
import numpy as np
A = np.array([[3,2,0],[-1,-3,6],[2,3,-5]])
invA = np.linalg.inv(A)
#print(A)
#print('------')
#print(invA)
#2. 함수로 구현하기...인데 복잡하니까 그냥..넘파이로 하자...
def inv(A):
n = len(A)
x = deepcopy(A)
#여인수행렬만들기
C=[]
for i in range(0,n):
row_C = []
#전체 행렬에서 i행 제외한 부분 행렬 인덱스
idx_r = list(range(0,n))
idx_r.remove(i)
#전체 행렬에서 j행 제외한 부분 행렬 인덱스
for j in range(0,n):
idx_c = list(range(0,n))
idx_c.remove(j)
#부분행렬
M=[]
for k in idx_r:
row_M=[]
for l in index_c:
val=X[k][l]
row_M.append(val)
M.append(row_M)
#부분행렬 행렬식
Mij = det_rec(M)
#여인수 구하기
Cij = ((-1)**(i+j)*Mij)
row_C.append(Cij)
#여인수행렬 구하기
C.append(row_C)
#수반행렬 만들기
adj = transpose(C)
res = scalar_mul(1/det_rec(X),adj)
return res'👩💻LEARN : ML&Data > Book Study' 카테고리의 다른 글
| [딥러닝 파이토치 교과서] #4. 딥러닝 시작 (0) | 2023.04.11 |
|---|---|
| [알고리즘 구현으로 배우는 선형대수] #7. 기저와 차원 (0) | 2023.04.10 |
| [알고리즘 구현으로 배우는 선형대수] #5. 행렬식 (0) | 2023.04.10 |
| [딥러닝 파이토치 교과서] #1. 파이토치 기초 (0) | 2023.04.09 |
| [알고리즘 구현으로 배우는 선형대수] #4. 선형 시스템 (0) | 2023.04.08 |