
🐍👣
라떼는 말이죠...문과가 미적분을 안배웠던 시절이었읍니다....
개념이나 사용하는 수식 자체가 어렵진 않은데 그 개념과 수식을 도출하기까지의 과정을 이해하자니
한권의 책으론 역부족이었다. (현재 보고 있는 책은 그닥 친절하지 않았다)
이에 나중에 보려고 했던 미분적분 책을 병행하면서 겨우 개념과 수식을 이해했는데, 과연 이걸 내가 직접 어떻게 쓸 수 있을지는 두고봐야겠따 흑흑...그냥 빨리 딥러닝 배우고 싶다 흑흑...
#3. 미분과 적분의 이해와 응용
(feat. [Book] 다시 미분 적분)
[미적분을 위한 사전 지식]
- 합성함수 : f(x)를 '특정 날짜의 판매량'을 알 수 있는 함수, g(x)를 '판매량에 따른 영업이익'을 알 수 있는 함수 라고 가정했을 때 특정 날의 영업이익을 알고자 하면 g(f(x)) 형태를 취해야 한다. 이를 합성함수라고 한다.
- 함수의 극한 : 함수의 입력값이 어느 특정한 값에 아주 가까워질 때 함수가 갖는 값
- f(x)에서 x가 a에 아주 가까워지면 f(x)의 값이 p에 가까워진다
- 극한 값 계산하기 (미분계수, 도함수와 유관)
- f(x)에서 분자가 x의2제곱 이상으로 구성되어있을 경우 인수분해한다
- 분모의 값을 0으로 만드는 성분이(x-a라던가..) 분자에도 있다면 (보통 있음), 이를 약분해서 없앤다
- 남은 분자의 x에 a를 대입하여 값을 구한다.
- 함수의 연속성 : 함수의 극한을 성립하기 위한 필요조건. 함수 그래프가 끊임없이 매끄럽게 이어지는 것을 의미함.
- 중간값 정리 : 임의의 함수 f(x)가 x=a, x=b 사이 연속이고 f(a)=/f(b)일 때 f(a)와 f(b) 사이의 임의의 값 k에 대하여 f(c)=k가 하나 이상 존재 한다는 의미
[미분의 이해]
... 너무 많은 설명이 압축되어 있어서 다른 책으로 공부하고 왔따 ..
📌「다시 미분 적분」에서 더 이해하기 위해 학습한 내용
1. 미분계수
- 전제1. 미분은 함수를 미세하게 나누어 분석하는 것으로 x의 변화량을 한없이 작게 만들었을 때 평균 변화율(f(b)->f(a))이 어떻게 되는 지를 보는 것이다
- 전제2. x의 변화량(b-a)을 한 없이 작게 만들면 두 점을 연결하는 기울기가 x=a에서의 f(x)와 맞닿은 접선이다
- 결론. 미분계수(f'(a)) = x의 변화량(b-a)을 한없이 작게, 극한에 가깝게 만들면 도달하는 접선의 기울기
- 이 때 x의 변화량 (b-a)가 한없이 작아지려면 b가 a에 가까워져야한다
- b와 a 사이의 거리를 h라 가정했을때
- b-a = h (h는 한없이 0에 가까워짐)
- b=a+h 이므로 두번째 식으로 변환할 수 있다.


- 미분계수의 공식 (p.79)
- 2항정리와 조합을 활용해야 함

- 상수함수 (f(x)=3 이런 거)의 경우 기울기가 0이기 때문에 x의 변화량에 따른 f(x)의 변화량도 0이므로 상수함수의 미분계수는 0이다.
2. 도함수

- 개념 : 미분계수를 x의 함수로 생각한 것. 사실상 함수 f(x)를 미분한다라는 것은 도함수 f'(x)를 구한다는 뜻
- 공식 : 위에 작성한 미분계수 공식의 a를 x로 바꿔주면됨.
△는 증가량을 나타내는 기호로 difference 첫글자를 따서 d라고도 한다
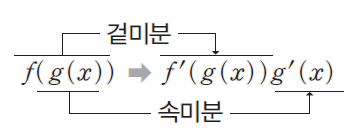
3. 합성함수 미분
- 개념 : 합성된 두 함수를 겉미분과 속미분으로 계산하고 이 두 개를 곱하는 것
# Sympy로 미분하기
import sympy as sp
x = sp.Symbol('x')
print(sp.diff(3*x**2 + 1, x)
#Scipy로 미분하기
from scipy, misc import derivative
#피미분함수
def f(x):
return 3*x**2+1
#미분한 함수
def d(x):
return derivative(f,x)
#x=2일때 미분값
print(d(2,0))
[적분의 이해]
.. 적분 또한 너무 많은 설명이 압축되어 있었다
📌「다시 미분 적분」에서 더 이해하기 위해 학습한 내용
1. 적분의 원리 (p.228)
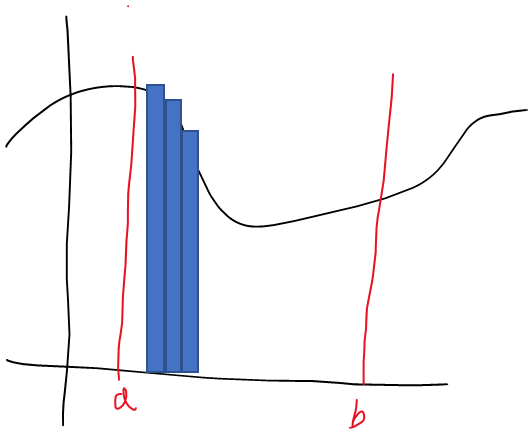
- f(x)라는 함수에서 a와 b사이의 넓이를 구한다고 했을 때 작은 직사각형(동일한 가로길이인 h )들을 합한다고 생각
- 하나의 직사각형의 넓이는
- h * f(a+kh) (k=0,1,2,,,,n-1)
- 모든 직사각형 넓이의 합은
- S = f(a)h + f(a+h)h + f(a+2h)h + f(a+3h)h ... + f(a(n-1)h)h
- 이 때 F'(x) = f(x)일 때 총 넓이인 S = F(b) - F(a) 를 보여야 함

이 때 F(a+nh)-F(a) 가 위에서 구한 S의 넓이와 동일함을 확인할 수 있었음 .
즉
S = F(a+nh)-F(a)
이때 a+nh=b라 두면
S = F(b)-F(a)임을 확인할 수 있게 됨
>> F(x)를 미분한 F'(x)를 f(x)라 하면, f(x)를 적분하게 되면 F(x)가 된다
>> 적분이란 f(x) * dx를 합하여 전체의 넓이를 구하는 것
2. 적분

2.1 부정적분 계산 방법
- x**2를 미분하면 2x가, 2x를 적분하면 x**2가 됨
- x**2+C를 미분해도 2x가 되며, 이 때의 2x를 적분하면 x**2+C가 됨
- 하지만 계수가 없는 경우도 있음 이 경우엔 이 다음의 식을 따름
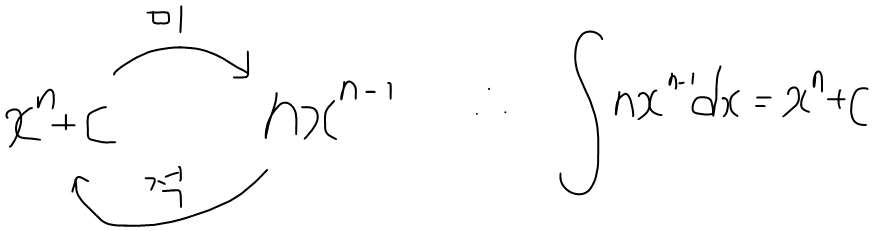
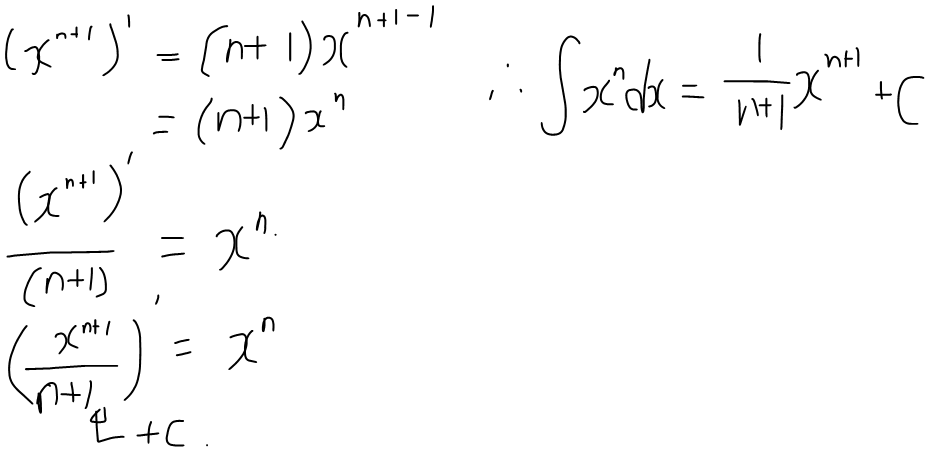
2.2 정적분
- f(x)라는 함수가 있을때
- 이를 적분하면 F(x), 원시함수
- 이를 미분하면 f'(x), 도함수
- 정적분이란
- f(x)의 원시함수 F(x)에 대해 F(b)-F(a)의 계산을 f(x)를 피적분함수로 하는 x=a부터 x=b까지의 정적분이라고 하고 아래처럼 표기함
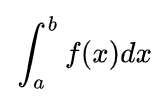
#심파이 integrate 사용해서 적분하는 법
import sympy as sp
x = sp.Symbol('x')
sp.integrate(3.0*x**2+1,x)
#사이파이 라이브러리로 적분하고 x가 0-2일때의 적분값 구하기
import numpy as np
from scipy.integrate import quad
def f(x):
return 3.0*x**2 +1
i = quad(f,0,2)
print(i[0])
[미적분학 기본 정리, 편미분]
- 미적분학 기본 정리
- 정적분이 F(b)-F(a)이며 (위의 정적분 정리 참고)
- f'(x) = dy/dx
- dy = d * f(x) = f'(x) * dx 임을 의미한
- 편미분
- 함수 z=f(x,y)처럼 두개 이상의 변수를 가지는 함수를 미분한 것을 의미
- y를 상수로 고정하는 경우 z는 x로만 구성된 1변수 함수로 보고 x에 대한 도함수를 얻는 것. 이렇게 얻어진 도 함수를 f의 x에 관한 편도함수라고 한다.
- 그라디언트 벡터 ( f(x,y,z) ) : 다변수 함수에서 여러개의 편도함수를 구할 수 있고, 다변수 함수의 모든 편도함수를 한 묶음으로 표현하는 것
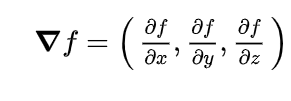
[분석모형 응용-경사하강법과 뉴턴랩슨 메서드]
- 전제 : f(x)에서 특정한 목적 (e.g. 최고의 만족도, 최저의 가격)을 확인하기 위해 기울기를 통해 해당 지점을 발견하려 한다
- 경사 하강법 : 미분을 활용하여 최적의 값을 찾는 법
- 함수 위의 임의의 점에서 시작하여 함수에서 계산한 기울기의 반대방향으로 움직여가며 국소 및 전역 최솟값에 도달하는 방법.
- e.g. 뉴턴랩슨 메서드 : 방정식의 해를 수치적으로 찾는 대표적인 방법
#경사하강법으로 방정식의 최소값 구하기
cur_x=3 # x=3에서 시작
rate = 0.01 #x축에서 움직여보는 최솟값. 학습률
precision = 0.000001 #반복계산에 사용할 기준으로 이전 단계의 x와 새로 계산한 x의 차이가 기준보다 작아지면 계산을 멈춘다
previous_step_size = 1
max_iters = 10000
#반복횟수 기록용
iters = 0
# 현재 x=3에서의 함수의 기울기
df= lambda x:2*(x+5)
#반복문
while(previous_step_size > precision) and (iters < max_iters) :
prev_x = cur_x #현재 x를 이전단계 x로 저장
cur_x = cur_x - rate*df(prev_x) #경사하강법 계산
previous_step_size = abs(cur_x - prev_x) #x값의 변화
iters = iters+1'👩💻LEARN : ML&Data > Book Study' 카테고리의 다른 글
| [머신러닝을 위한 수학 with 파이썬, R] #5. 확률분포와 통계적 추론 (0) | 2023.01.30 |
|---|---|
| [머신러닝을 위한 수학 with 파이썬, R] #4. 확률과 통계 (2) | 2023.01.29 |
| [머신러닝을 위한 수학 with 파이썬, R] #2. 머신 러닝을 위한 선형 대수 part2. 고윳값, 고유벡터, 대각화 (1) | 2023.01.26 |
| [머신러닝을 위한 수학 with 파이썬, R] #2. 머신 러닝을 위한 선형 대수 part1. 벡터, 내적외적, 역행렬 (0) | 2023.01.24 |
| [머신러닝을 위한 수학 with 파이썬, R] #1. 데이터 과학과 파이썬 소개 (0) | 2023.01.24 |
