[머신러닝을 위한 수학 with 파이썬, R] #4. 확률과 통계

 

🐍👣

배우지 않았던 선형대수와 미적분을 3일에 걸쳐서 끝낸 이유일까... 확통? 완전 자쉰있쯰~~~라고 했지만 수식만 보면 겁에 질리는 사람 그 사람이 바로 나에요

시그마 너무 공격적으로 생김;

 

---

#4. 확률과 통계 

※ 확통 내용 중 기본적으로 알 만한 내용은 모두 건너뛰고 기억해야 할 개념 및 수식 위주로 정리 

 

• 분산 : 각 관측값이 평균에서 얼마나 퍼져있는 지를 보는 척도 

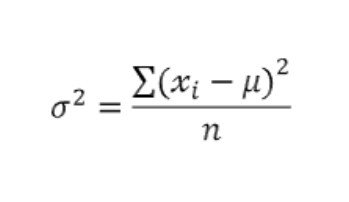
• 표본분산 : 표본에서 얻은 분산 
  • 모분산과 달리 n-1을 분모로 사용하는 이유는 분산을 계산할 때 모평균이 아닌 표본 평균을 사용했기 때문에 모집단의 편의 추정량(biased estimator)이 되므로, 분산이 불편 추정량(unbiased estimator)이 되도록 하기 위해서이다 [위키백과] 

• 표준편차
  • 각 관측값이 평균과 대체로 어느정도 차이나는지 보고 싶지만 분산은 평균과의 차이를 제곱한 값으로 크기가 제곱되어 나타나기 때문에 분산을 원래 알고자 하는 크기로 바꾸려면 분산값의 제곱근을 사용한 표준편차를 봐야 함 

• 공분산
  • 두 개 이상의 변수가 있을 때, 변수들이 각각의 평균으로 부터 떨어진 정도를 의미. 변수와 변수 평균 값의 차이를 구하고 이 차이들을 곱한 다음 n값으로 나눈 것 
  • 공분산이 0보다 크면 두 변수가 같이 증가, 0보다 작으면 반비례 
• 상관관계
  • 공분산만으로는 공분산이 큰 것이 실제 변수들의 증감 관계에 의한 것인지 아니면 각 변수의 크기에 영향을 받은 것인지 구분할 수 없어 등장한 개념 
  • 두 변수의 공분산을 바로 각 변수의 표준편차로 나눠 구함 to 각 변수의 절대적인 크기에 영향을 받지 않기 위해 

출처. 위키백과

• 표본공간 : 통계 조사에서 얻을 수 있는 모든 결과의 집합, 출현 가능한 모든 결과의 집합 
  • 이산형 표본 공간 : 표본 공간 안에 있는 원소(표본점)를 하나 씩 셀 수 있는 경우 
  • 연속형 표본 공간 : 표본 공간 안에 있는 표본점을 하나로 셀 수 없는 형태로 무한히 많은 공간 (e.g. 전구의 수명 시간)
• 조건부 확률 : Event A가 일어났을 때 Event B가 일어날 확률 
  • 단 A와 B가 독립일 경우 P(A교집합B) = P(A)P(B)이기 때문에 B의 조건부 확률은 P(B)가 됨 

• 베이즈 정리 : A의 확률이 존재할 때[사전확률], 새롭게 얻은 자료인 A와 B의 관계를 나타내는 확률[A가 주어진 경우 B의 조건부확률]을 이용하여 결과적으로 B가 주어진 경우 A의 조건부 확률[사후확률]을 구하는 것 
  •  이 때 P(B)는 B의 사전확률로 정규화 상수로서 역할 
  • 자세한 설명은 위키백과를 보는 것이 더 빠를 것 같다. (대충 수식 쓰기 귀찮음...정리유도 보면 이해 찰떡..)