
아 선생님 살려주세용
내적 자체는 안어렵네 했는데
직교 나오고 분해 나오면서 정신이 안드로메다로 가버렸어용
#8. 내적(inner product)
1. 내적의 개념
내적 공간
다음 공리를 만족하는 벡터 공간을 내적 공간이라고 한다.
- <u,v> = <v,u>
- <u+v,w> = <u,w>+<v,w>
- <a*u,v> = a<u,v>
- <u,v> >= 0
내적 정의
- 내적이란 벡터 간 연산의 한 종류로, 벡터와 벡터의 연산 결과로 스칼라가 나온다.
- 이 때 두 벡터 간 n*p , p*m 형태여야 하는데 그렇지 못할 경우 (p*n등)한 행렬을 전치시켜서 내적 연산을 수행한다.
내적 성질
- 내적 → 벡터의 길이(norm) , 벡터 사이 관계 파악 가능
- 벡터 사이의 관계
- 내적 > 0 → 두 벡터 사이의 각도 <90
- 내적 < 0 → 두 벡터 사이의 각도 >90
- 내적 = 0 → 두 벡터 사이의 각도 = 90 ⭐️ (추후 직교와 연관)
- 벡터의 길이 (||u||)
- 벡터 u(u1,u2,u3...,un)이 있을 때
- ||u|| = 제곱근(u1**2 + u2**2 + u3**2+...+un**2)
- u=(u1,u2)이면
- 길이 = 제곱근(u1**2 + u2**2)
- 좌표 = (||u||*cosθ, ||u||*sinθ) 즉 x,y축이 있다고 햇을 때 x,y의 길이는 벡터u의 대각선 길이에 코사인,사인을 곱한 x축,y축의 좌표를 의미하는 것이다.
- 벡터 u,v 사이 간 내적을 삼각함수를 통해 확인해보면
- <u,v> = ||u||||v|| * cosθ
- 벡터 u와 벡터v의 길이를 곱한 것에 코사인을 취함 🤔
- ||u|| : 벡터 u의 대각선 길이
- ||v|| : 벡터 v의 대각선 길이
- cosθ : u가 v 방향으로 작용하는 크기를 의미
- u와 v를 내적한 것은 곧 벡터 u가 v방향으로 작용한 힘의 효율은 의미함
- 참고 : https://hub1234.tistory.com/48
- 벡터 u와 벡터v의 길이를 곱한 것에 코사인을 취함 🤔
- <u,v> = ||u||||v|| * cosθ
정사영
의미 : 한 벡터 공간에 속한 벡터를 부분 공간으로 수직 투영하는 것을 의미함
- 벡터 u,v가 있을 때 벡터 u를 벡터 v에 정사영 하게 되면
- 정사영한 결과값의 벡터를 projvu 라 하고
- 해당 벡터의 길이인 ||projvu|| = ||u||cosθ 이다.
- 정사영의 개념을 활용했을 때
- 벡터 u,v의 내적은 벡터u를 벡터 v에 정사영 시킨 벡터의 길이 (||u||cosθ)에 기존 벡터의 길이 ||v||를 곱한 것과 같다.
- 만약 내적의 결과가 음수라면 projvu가 v와 반대임을 뜻함
- 벡터 u,v의 내적은 벡터u를 벡터 v에 정사영 시킨 벡터의 길이 (||u||cosθ)에 기존 벡터의 길이 ||v||를 곱한 것과 같다.

2. 직교 공간과 정규 직교 공간
직교 공간(orthogonal)
- 직교 공간 : 벡터 공간에 존재하는 모든 벡터가 서로 직교(=두벡터의 내적 값은 0)하는 것을 의미함
- 직교 공간에 속하는 모든 벡터는 서로 직교함
- 이 때, 각 벡터의 길이가 모두 1이면 정규직교라고 함
정규 직교 공간
- 정규 직교 공간 : 정규 직교 벡터가 만드는 공간
- 모든 벡터 간 내적 값은 0
- 모든 벡터의 길이는 1
- 정규화 : 직교 벡터를 정규 직교 벡터로 변환 (becuase 길이가 1이라 연산이 쉬워짐)
- 직교 벡터를 해당 직교 벡터의 길이(norm)로 나눔
정규 직교 벡터를 활용한 좌표 표현
- 벡터 공간 v의 정규 직교 기저를 S= {v1,v2,v3,,,vn}이라 할때 벡터 공간v에 포함되는 임의의 a 벡터는 다음과 같이 표시한다
- a = <a,v1>v1 + <a,v2>v2+<a,v3>v3+...+<a,vn>vn = c1v1 + c2v2+...+cnvn
- v1,v2,,,vn = 좌표축 (기저니까!)
- <a,vi> = 벡터 a의 i번째 축의 좌표
- → a는 정규기저벡터 v들의 조합으로, <a,vn>이 스칼라값으로 나오는 것을 고려했을 때 c*x1+c*x2...처럼 선형 결합으로 간주할 수 있음
- → 즉 c들은 v를 기저(좌표축)으로 갖는 임의의 좌표! 라고 보면 됨
- <a,vn> = cn 임을 입증하기 위해선
- v들은 정규직교하므로 길이=1, 내적결과=0임을 감안했을 때,
- <a,vi> = <c1v1+c2v2+...cnvn , vi> = <c1v1, vi>+<c2v2, vi>+...<cnvn,vi>
- <a*u,v> = a<u,v>임을 이용했을 때 <cnvn,vi> = cn<vn,vi> = cn*0
- 이에 이 중 남는 것은 vi 자기자신과 내적한 결과인 <civi,vi>
- <civi,vi> = ci<vi,vi>=ci ( 자기자신과 내적할 경우 viT*vi = 항등행렬)
이게 맞나..?^^..?
칸아카데미의 도움을 받으니 자기자신과 내적할 경우 길이=1이라고 하는데 정규 직교하면 길이가 1인거지 자기 자신과와의 내적 결과는 길이인 1과 동일하다는 것인가..? 칸아카데미 한번 쫙 훑어보기..약속...나자신...
직교 벡터를 활용한 좌표 표현
- 벡터 공간 내 U={u1,u2,,,,un}이 직교기저라면 임의의 벡터 a는 다음과 같이 표현된다
- 이 때 벡터 a의 좌표가 u1...un의 계수로 이뤄짐을 알 수 있다.

- 증명해보자....🥲
- 직교기저 U를 정규 직교 기저 벡터로 변환시킨다 by 각자의 길이로 나누기
- un = un/||un||이 된다
- 이를 정규직교벡터를 활용한 좌표 표현으로 적용해보면
- a = <a,un/||un||>*un/||un|| 의 합이되며 이를 좀 더 정리해보면
- a = (<a,un> / ||un||**2) * un 의 합이 되어 맨 위의 수식처럼 표현할 수 있다.
- 직교기저 U를 정규 직교 기저 벡터로 변환시킨다 by 각자의 길이로 나누기
3. 그램 슈미트 과정
정사영 정리
벡터 공간 S의 부분공간 W가 존재할 때, W에 속하는 벡터를 w1, W의 직교공간인 W'에 속하는 벡터를 w2라고 하면
벡터 공간 S에 속하는 임의의 벡터 a는 a = w1 + w2 로 표현할 수 있다.무슨말이에요 이게
우선 공간 S는 차치하고 W와 W'만 있다고 가정하고 그리면 서적의 다음 그림처럼 그릴 수 있다.

- w1 = projwa : a를 W에 정사영한 벡터
- w2 = projw'a = a를 W'에 정사영한 벡터
- a = projwa + projw'a
직교 정사영
벡터 공간 S의 부분공간 W의 직교기저가 {u1,u2,...un}일때 a가 S의 임의의 벡터라면 a를 W에 정사영 시킨 벡터는 다음과 같으며, un 좌표측 앞의 계수들의 집합이 a의 좌표임을 알 수 있다.
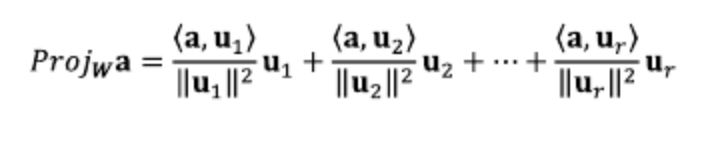
또한 벡터 공간 S의 부분공간 W의 정규직교기저가 {v1,v2...vn}이라 할 때, a가 S의 임의의 벡터라면 a를 W에 정사영 시킨 벡터는 다음과 같으며, vn 좌표측 앞의 계수들의 집합이 a의 좌표임을 알 수 있다.
- a = <a,v1>v1 + <a,v2>v2+<a,v3>v3+...+<a,vn>vn
그램 슈미트 과정
- 의미 : 기저 벡터인 {s1,s2,...sn}을 직교 기저 벡터인 {u1,u2...un}으로 변환하는 과정
- 기저를 직교 기저로 변환하는 것이므로 모든 벡터가 서로 직교하게 만들어야 함
1️⃣ 새로운 직교 기저 벡터 u1을 기존 기저 벡터의 첫번째 요소인 s1으로 정의한다
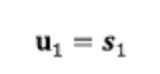
2️⃣ 처음 만든 직교 기저 벡터 u1과 직교하는 직교 기저 벡터 u2를 생성한다.
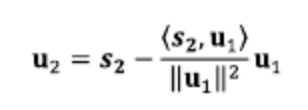
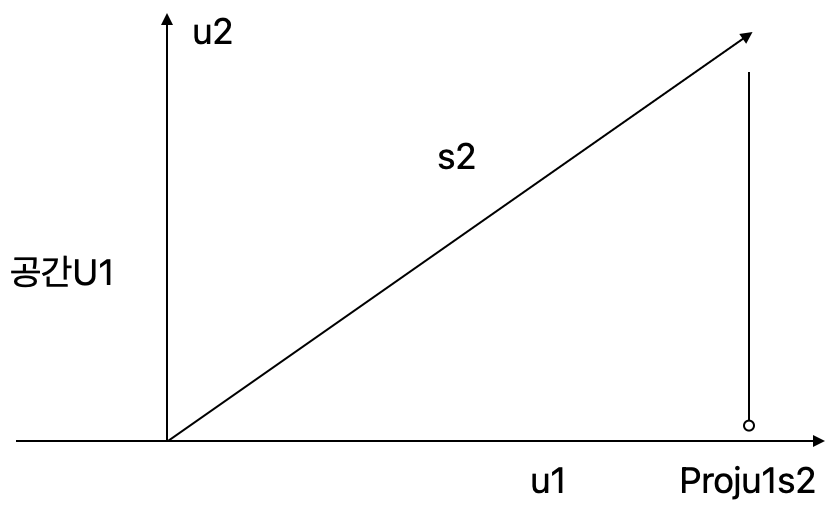
- u1이 생성하는 공간을 U1이라 했을 때,
- 직교기저벡터 u1에 직교하는 벡터 u2를 생성하기 위해 기존 두번째 기저 벡터 s2를 기저 벡터 u1이 생성하는 공간 U1에 정사영 시킴
- 즉 s2 = u2+proju1s2 이므로 (???????why...)
- u2 = s2 - proju1s2
3️⃣ u3는 앞서 생성한 u1,u2와 직교하도록 생성한다.
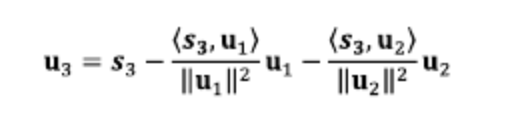
- u3 = s3 - proju2s3이므로 위와 같으며 이를 일반화한 식은 아래와 같다.
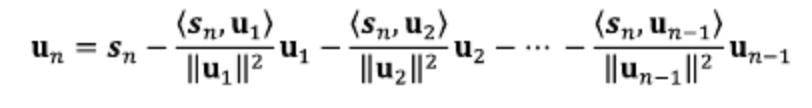
4. QR 분해
기본적인 QR 분해 방법
- A가 nxp 행렬이고 풀 랭크 (열 벡터가 모두 선형 독립)일 경우, 행렬 A를 다음과 같이 분해할 수 있다.
- A = QR
- Q : nxp 행렬이며 정규 직교 벡터들로 구성됨 (벡터간 내적=0, 길이들은1)
- R : 가역 상 삼각행렬
- 방법
- 행렬 A의 열벡터 {a1,a2,...an}이 있고 A의 정규 직교 벡터 {v1,v2...vn}이 있을 때, v들을 해당 공간의 좌표축이라 보고 a를 v의 선형 결합이라고 보면
- 열 벡터의 표현식은 다음식으로 표현할 수 있다.
- a1 = <a1,v1>v1 + <a1,v2>v2 + <a1,v3>v3+..+<a1,vn>vn
- <a1,vn>vn : 열벡터 a1의 n번째 좌표
- a2 =<a2,v1>v1 + <a2,v2>v2 + <a2,v3>v3+..+<a2,vn>vn
- a1 = <a1,v1>v1 + <a1,v2>v2 + <a1,v3>v3+..+<a1,vn>vn
- 이를 행렬로 표현하면 다음과 같다.
- (a1 a2 ... an ) = (v1 v2 ... vn) * ([<a1,v1>, <a2,v1>...<an,v1>], [<a1,v2>, <a2,v2>...<an,v2>],[<a1,v3>...]
- 그램슈미트 과정에 의해
- 정규직교벡터 vj는 벡터 a1,a2,,,,,,aj-1 과 직교한다.
- 그러므로 <a1,vj>...<aj-1,vj>까지의 값은 모두 0이므로 하삼각행렬에 해당하는 영역은 모두 0이 된다.
- 그러므로 A는 정규직교 벡터 v로 구성된 Q와 가역상삼각행렬 R로 분해할 수 있다.
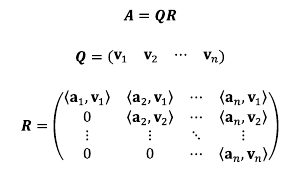
하우스 홀더 방법을 이용한 QR 분해
하우스 홀더 행렬을 이용해 주어진 행렬을 QR분해하는 것
- 🤔하우스 홀더 행렬...?
- 어떤 행렬을 다른 형태로 변환할 때 사용하는 행렬로, 하우스 홀더 행렬은 정사각 행렬이며 모든 열이 정규 직교한다는 특징
- v=(v1,v2,...vn)의 nx1행렬이 있을 때, 하우스 홀더 행렬은 I(항등행렬) - 2 * {(v*vt)/(vt*v)}을 따른다.
- 방법 (복잡..)
- 주어진 행렬 A가 있을 때
- A1=A라고 가정
- A1의 1열을 a1이라 설정하고, 다음 값들을 구한다.
- ||a1|| : 벡터 a1의 길이(norm)
- sign(a1) : 벡터 a1의 첫번째 원소의 부호를 의미하며 a1>=0 이면 +1, a1<0이면 -1
- e1 : 기저벡터
- 왜인진 모르겠으나 a1과 같은 shape이되 첫원소가1이고 나머지가 다 0이면 되는듯
- v1 = 벡터 a1 + sign(a1) * ||a1|| * e1 = a1과 같은 형태의 벡터로 도출됨
- 하우스홀더 행렬 H1 = I- 2 * {(v1*v1t)/(v1t*v1)}를 구한다
- A1의 1열을 a1이라 설정하고, 다음 값들을 구한다.
- A2 = H1*A1 결과에서 1행 1열을 모두 제거한 행렬
- HnAn이 벡터가 될때 까지 앞의 내용을 반복
- n개의 하우스홀더행렬 H1,H2,H3을 구한다.
- R = H3H2H1A 임
- 이때 H간 shape이 다른 문제는, 모자란 1행 1열, 2행 2열에 항등 행렬 원소를 임베딩해주는 방법으로 보완
- A = QR = (H1H2H3) * (H3H2H1)
이렇게까지해야하나요?ㅠ
5. 파이썬 실습
정신이아득해져서 넘파이 라이브러리만 시도해보려 한다...
import numpy as np
#1. 기본 내적
a = np.array([1,2,3])
b = np.array([4,5,6])
res = np.inner(a,b)
#32
#2. QR분해
A = np.array([1,0,1],[0,1,1],[1,2,0])
Q,R = np.linalg.qr(A)
#이게..끝...?'👩💻LEARN : ML&Data > Book Study' 카테고리의 다른 글
| [알고리즘 구현으로 배우는 선형대수] #10. 고유값과 고유벡터 (0) | 2023.04.13 |
|---|---|
| [알고리즘 구현으로 배우는 선형대수] #9. 다양한 곱 연산 (0) | 2023.04.13 |
| [딥러닝 파이토치 교과서] #4. 딥러닝 시작 (0) | 2023.04.11 |
| [알고리즘 구현으로 배우는 선형대수] #7. 기저와 차원 (0) | 2023.04.10 |
| [알고리즘 구현으로 배우는 선형대수] #6. 역행렬 (0) | 2023.04.10 |