728x90

#2. Anomaly detection
▶️ Finding unusual events
새로운 데이터셋이 기존의 데이터 plot과 유사한 곳에 있지 않을 경우, anomaly 하다고 판단할 수 있다

Density estimation
- 기존 데이터로 모델 P(x)를 학습시킨 이후 새로운 X가 데이터셋에서 나타날 확률을 P(X)라고 한다.
- 이때 P(X)가 epsilon(작은수)보다 작을 경우 anomaly로 분류한다

▶️ Gaussian (normal) distribution
- 정규분포! 평균(Mu), 표준분포(sigma, 분산은 sigma**2)로 이뤄진 종모양 분포
- x의 확률을 구하는 식은 p(x)이며, x가 중심에서 멀어질수록 p(x)도 낮아진다.

Parameter estimation
- dataset이 주어졌을 때 평균과 분산을 구할 수 있음
- x가 평균에서 멀리 있을 수록 anomaly하다고 볼 수 있다.

▶️ Anomaly detection algorithm
공식
- n개의 feature를 가진 x의 벡터가 있다고 가정했을 때, x의 확률은 모든 p(x)를 곱한 것으로 아래와 같다.
- p(xn)의 확률을 나타내기 위해 평균과 분산을 함께 기재해준다

방법
1. Anomaly에 대한 indicator가 될 수 있을 것으로 보이는 n개의 feature x를 선택한다.
2. 모든 x에 대해 평균과 분산을 구한다
3. 새로운 x가 주어졌을때 해당 x의 p(x)를 구하고, 만약 P(x)가 e(엡실론)보다 작으면 anomaly로 본다.

- feature x1,x2에 대한 확률과 분산을 구했을 때 3D 이미지로 표현되며, 해당 이미지에서 평균과 떨어져있을 수록 anomaly로 보임을 확인
▶️ Developing and evaluating an anomaly detection system
Developing
- Train / cv / test set으로 나눈다
- Train : y 는 없으며, 알고리즘을 학습시키는데에 사용한다
- cv : 소수의 anomaly (y label)를 포함하여 사용, cv로 사용하되 엡실론을 tune하는데 사용할 수 있다
- test : cv와 유사하게 소수의 anomaly를 포함하여 사용한다
Evaluating
- x feature들을 바탕으로 p(x)를 학습시킨다
- cv/test set에서 예측한다
- p(x)가 엡실론보다 작으면 → y = 1
- p(x)가 엡실론과 같거나 크면 → y=0
- 이 때 anomaly의 수는 매우 작으므로 Skewed data 이며, 이럴 경우 다음과 같은 방법을 활용하여 평가할 수 있다.
- F1-score (using Precision, Recall)
- CV Set에서 테스트를 진행하며 F1 score 를 최대로 하는 엡실론 값을 도출할 수 있다.
▶️ Choosing what features to use
Anomaly detection에 중요한 것은 적합한 feature를 선택하는 것
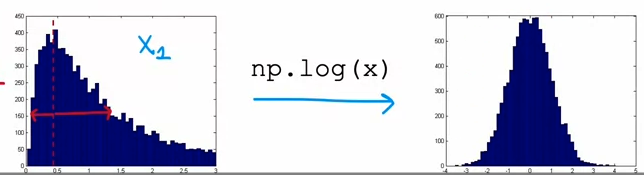
Non gaussian features
선택한 feature가 가우시안 분포에 해당하지 않는다면, 가우시안으로 만든다! by log(x) log(x+c), x**(1/n) 등
Error analysis for anomaly detection
대부분의 anomaly data는 하나의 feature만 보았을 때 p(x)가 엡실론보다 크게 나올 수 있다
이에 다른 feature를 함께 보면 (n차원) anomaly를 보다 쉽게 확인할 수 있다.
이에 새로운 feature를 다른 feature들간의 조합으로도 확인할 수 있다.
#1. 가우시안 분포 계산하기
def estimate_gaussian(X):
m, n = X.shape
### START CODE HERE ###
mu = np.sum(X, axis=0) * (1/m)
var = np.sum((X-mu)**2, axis=0) * (1/m)
### END CODE HERE ###
return mu, var
# 참고
# Returns the density of the multivariate normal
# at each data point (row) of X_train
p = multivariate_gaussian(X_train, mu, var)
#2. 엡실론값 구하기 with F1 score
def select_threshold(y_val, p_val):
"""
Finds the best threshold to use for selecting outliers
based on the results from a validation set (p_val)
and the ground truth (y_val)
Args:
y_val (ndarray): Ground truth on validation set
p_val (ndarray): Results on validation set
Returns:
epsilon (float): Threshold chosen
F1 (float): F1 score by choosing epsilon as threshold
"""
best_epsilon = 0
best_F1 = 0
F1 = 0
step_size = (max(p_val) - min(p_val)) / 1000 #엡실론값 만들기용
for epsilon in np.arange(min(p_val), max(p_val), step_size):
### START CODE HERE ###
predictions = (p_val < epsilon) #반환값 = 0, 1
tp= sum((predictions == 1) & (y_val == 1)) #true-positive
fp= sum((predictions == 1) & (y_val == 0)) #false-positive
fn= sum((predictions == 0) & (y_val == 1)) #false-negative
prec= tp / (tp+fp)
rec= tp / (tp+fn)
F1 = ( 2 * prec * rec ) / ( prec + rec )
### END CODE HERE ###
if F1 > best_F1:
best_F1 = F1
best_epsilon = epsilon
return best_epsilon, best_F1
p_val = multivariate_gaussian(X_val, mu, var)
epsilon, F1 = select_threshold(y_val, p_val)