
이 강의 오리지널 버전(코세라 처음 생겼을 쯤)을 듣다가 말았었는데, 그때 그냥 진작에 들을걸...
물론 지금이 강의자료도 더 많고 번역본도 많아서 공부하긴 편하지만 그때 알아뒀으면 출발선이 지금보단 훨씬 앞에 있을 것 같다 흑흑
#2. Regression Model
Linear regression model
기존 데이터들에 기반하여 예측선을 그리고, New input이 들어왔을때 해당 선에 매칭되는 output을 예측값으로 하는 것
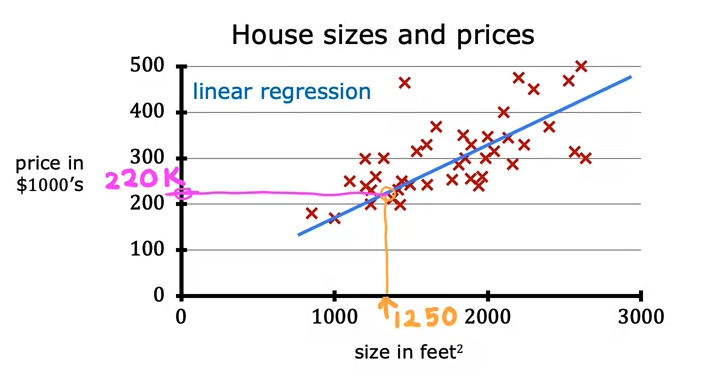
Process
training set (x : features, y : targets) -> learning algorithms(F, 즉 모델) 구축
-> new x(feature)를 모델에 넣어 y(prediction)을 도출하는 것
- f(x) = w * x + b
Notation
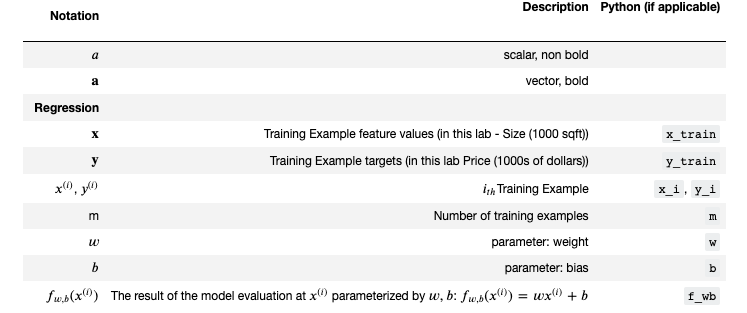
- print(f"문자열어쩌구저쩌구 {변수}")
#linear regression 모델 만들고 그래프 그리기
x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])
w = 100 #가상으로 가중치와 절편 선언
b = 100
def compute_model_output(x,w,b):
m = x.shape[0]
f_wb = np.zeros(m) #0 으로 생성된 가상의 배열 생성
for i in range(m):
f_wb[i] = w * x[i] + b
return f_wb
tmp_f_wb = compute_model_output(x_train,w,b)
# Plot our model prediction
plt.plot(x_train, tmp_f_wb, c='b',label='Our Prediction')
# Plot the data points
plt.scatter(x_train, y_train, marker='x', c='r',label='Actual Values')
# Set the title
plt.title("Housing Prices")
# Set the y-axis label
plt.ylabel('Price (in 1000s of dollars)')
# Set the x-axis label
plt.xlabel('Size (1000 sqft)')
plt.legend()
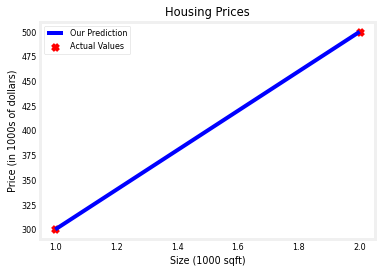
plt.show()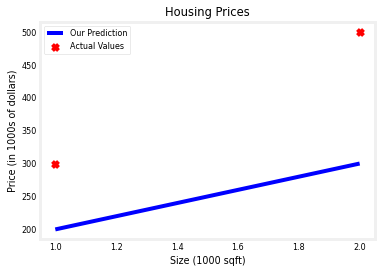
Cost function formula
- Cost function = 비용함수 (오차함수는 Loss function)
1. Parameter
- w : 가중치, 기울기 = weights
- b : 절편
-> w,b에 따라 training set의 데이터를 설명하는 선이 달라지므로, 해당 선이 training data를 얼마나 잘 설명하는지 알 수 있어야 함
2. Cost function ( = J(w,b), Squred error cost function )
모든 training data의 y 오차(예측값-실제값)의 제곱을 합치고 이의 평균을 구함 = 예측값이 실제값을 얼마나 잘 예측했는지 보여줌
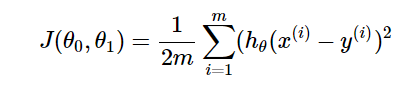
Cost function intuition
결국 cost function 을 최소화하여, training data를 가장 잘 설명하는 선을 만들고자 하는 것
문제를 간단하게 보기 위해 b = 0이라고 가정하고 보게 되면
J(w) = 1/2m * 시그마 ( w* x(i) - y(i))^^2가 됨
training dataset = ((1,1),(2,2),(3,3))이라 가정, w=1이라 가정 시
J(1) = 1/2m (0들의합) = 0이 됨. w의 값을 증감해가며 해당 그래프를 그리면 아래와 같이 포물선모양의 그래프가 됨
해당 그래프의 최저점 즉 꼭지점 = J(w)가 최소가 되는 지점을 찾아야 함
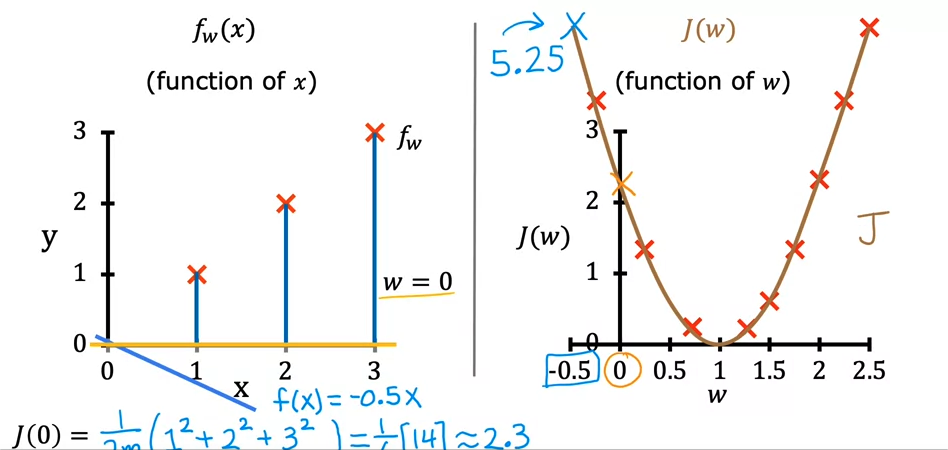
Visualizing the cost function
다시 돌아와서 b가 값을 가지고 있다고 가정하고, Cost function의 그래프 (F, J)를 비교...했는데...
변수가 w,b 두개에 y값이 있다보니 3차원이 됨. 대충 위의 포물선 그래프가..3차원이되었다...볼수있겠음
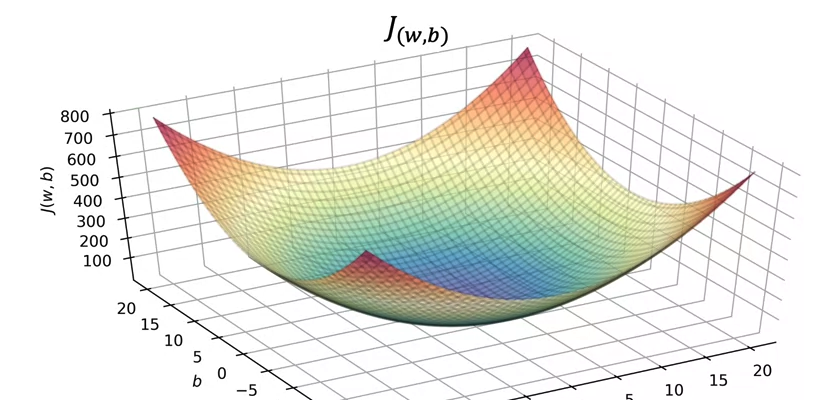
그런데 이렇게 3D로 보면 헷갈리니까 등고선 그래프(Contour plot) 형태로 보면 결국 가장 가운데로 수렴하는 타원 → 미니멈이 됨
기존 F 그래프와 J의 등고선 그래프를 그려보면 아래와 같음.
→미니멈에 가까워지는 J의 지점으로 갈 수록 F에 fit한 예측선을 그려나가는 것을 확인할 수 있음
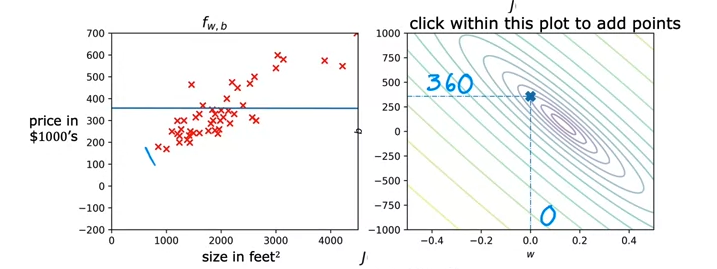
# 비용함수 구현
def compute_cost(x, y, w, b):
# number of training examples
m = x.shape[0]
cost_sum = 0
for i in range(m):
f_wb = w * x[i] + b
cost = (f_wb - y[i]) ** 2
cost_sum = cost_sum + cost
total_cost = (1 / (2 * m)) * cost_sum
return total_cost
#3. Gradient descent
(경사하강법!)
Gradient descent
우리의 목적 : w,b를 J(w,b)를 최소로 만드는 값으로 찾아나가는 것
→ Gradient Descent = 방향을 점검하며 최소지점으로 이동해나가는 것. 이를 여러번 반복
위의 3차원 그래프에서 gradient descent를 사용했다면,
1️⃣ 최초의 위치 선정 (보통 w,b가 0,0인것을 선택)
2️⃣ 최소값에 도달하기 위한 방향을 설정한 후 baby little step(ㅋㅋㅋㅋ)으로 다가가는 것을 반복
3️⃣ 최소값도달! 하고 이를 다시 반복함 (위치를 변경하거나 방향을 번경하거나 등등)
Implementing gradient descent
알고리즘 (about w, b)
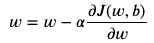
- 알파 = learning rate. step의 보폭을 결정
- 알파 뒤에 있는 애 = Derivative of J. 미분값은 기울기이며 기울기의 방향(+,-)에 따라 가는 방향이 달라짐
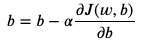
- b의 경우에는 J를 b로 미분한 값
→ 결국 이 w,b를 계속 업데이트해나가며 최소값을 찾아가는것
※ 유의사항
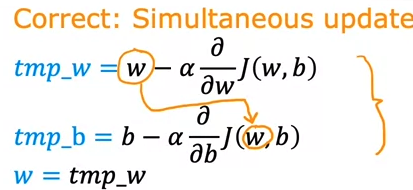
w,b를 동시에 업데이트해나가는 것은 맞으나, w가 업데이트된 값을 바로 b에서 미분하는 것이 아님. b를 업데이트할 때 tmp_w를 쓰지 않도록 유의하자
Learning rate
학습률이 너무 작으면 최소값까지 반복수가 커지고 느려짐.
학습률이 너무 크면 J의 최소값이 아니라..발산할수가 있음;
학습률은 그럼 어떻게 결정하는가! (= 어떤 조건에서 업데이트를 멈추고 최소값에서의 파라미터를 반환할 것인가)
→ 최초 세팅 값에서는 기울기가 클 수 밖에 없으나 최소값에 가까워질수록 포물선 그래프의 특성 상 기울기가 작아지며 비록 학습률이 fixed되어잇을 지언정, step의 폭은 점점 작아질 수 밖에 없음.
→ 최소값에 가까워질수록 step의 폭은 0에 수렴할 것이며 직전의 step과 큰 차이가 나지 않을 것임. 포물선 그래프에서 최소값에 접하는 기울기는 0 (= 미분값이 0). 이때의 파라미터가 최소값을 도출하는 파라미터
Gradient descent for linear regression
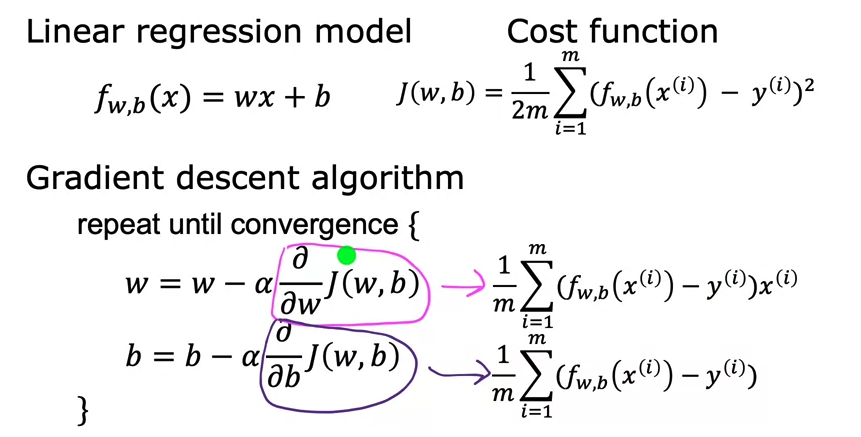
도출방식
- J(w,b)를 그냥 w,b를 인자로 가진 Y라 가정하면 결국 dy/dw, dy/db에 대한 수식이라고 볼 수 있음
- dy/dw의 경우, y를 기존에 정의한 수식을 대입한 이후, 이의 도함수를 구해주면 됨.
- 시그마는 무시하고, 일차방정식을 제곱한 함수 즉 합성함수의 미분을 수행.
- 아래의 방식과 같이, 지수 2와 x(i)가 앞으로 내려오게 됨 (w에 대해 미분하는 것이므로 x(i)는 상수로 취급)
- dy/db의 경우 b에 대해 미분했을 시 b에 곱해진 상수는 1 외엔 없으므로 dy/dw와 다른 결과가 도출됨
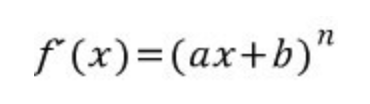
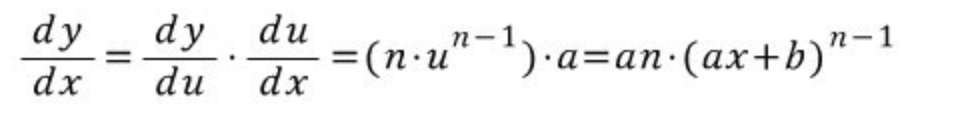

Running gradient descent
Batch Gradient Descent Algorithm
경사하강을 업데이트 시 모든 training set을 활용. subset만 사용하는 것도 가능하나 linear regression에서는 전체를 사용
#기울기 구하는 코드
def compute_gradient(x, y, w, b):
"""
Computes the gradient for linear regression
Args:
x (ndarray (m,)): Data, m examples
y (ndarray (m,)): target values
w,b (scalar) : model parameters
Returns
dj_dw (scalar): The gradient of the cost w.r.t. the parameters w
dj_db (scalar): The gradient of the cost w.r.t. the parameter b
"""
# Number of training examples
m = x.shape[0]
dj_dw = 0
dj_db = 0
for i in range(m):
f_wb = w * x[i] + b
dj_dw_i = (f_wb - y[i]) * x[i]
dj_db_i = f_wb - y[i]
dj_db += dj_db_i
dj_dw += dj_dw_i
dj_dw = dj_dw / m
dj_db = dj_db / m
return dj_dw, dj_db
#경사하강법 수행 코드
def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function):
"""
Performs gradient descent to fit w,b. Updates w,b by taking
num_iters gradient steps with learning rate alpha
Args:
x (ndarray (m,)) : Data, m examples
y (ndarray (m,)) : target values
w_in,b_in (scalar): initial values of model parameters
alpha (float): Learning rate
num_iters (int): number of iterations to run gradient descent
cost_function: function to call to produce cost
gradient_function: function to call to produce gradient
Returns:
w (scalar): Updated value of parameter after running gradient descent
b (scalar): Updated value of parameter after running gradient descent
J_history (List): History of cost values
p_history (list): History of parameters [w,b]
"""
# An array to store cost J and w's at each iteration primarily for graphing later
J_history = []
p_history = []
b = b_in
w = w_in
for i in range(num_iters):
# Calculate the gradient and update the parameters using gradient_function
dj_dw, dj_db = gradient_function(x, y, w , b)
# Update Parameters using equation (3) above
b = b - alpha * dj_db
w = w - alpha * dj_dw
# Save cost J at each iteration
if i<100000: # prevent resource exhaustion
J_history.append( cost_function(x, y, w , b))
p_history.append([w,b])
# Print cost every at intervals 10 times or as many iterations if < 10
if i% math.ceil(num_iters/10) == 0:
print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",
f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e} ",
f"w: {w: 0.3e}, b:{b: 0.5e}")
return w, b, J_history, p_history #return w and J,w history for graphing
# initialize parameters
w_init = 0
b_init = 0
# some gradient descent settings
iterations = 10000
tmp_alpha = 1.0e-2
# run gradient descent
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha,
iterations, compute_cost, compute_gradient)
print(f"(w,b) found by gradient descent: ({w_final:8.4f},{b_final:8.4f})")