728x90
정규분포가 여러개 있는 다차원의 정규분포를 의미
1. 다변량 표준정규분포
- 가정 : 표준정규분포를 따르는 i.i.d한 확률변수 Z1,Z2,,,Zn을 늘어놓은 열 벡터 Z가 따르는 분포를 n차원의 표준분포라고 함
- Z의 확률밀도 함수

- Z의 기댓값 벡터와 공분산행렬
- 각각의 확률변수 Z1,Z2..Zn이 모두 표준정규분포를 따르고 독립이므로
- E[Zn] = 0, V[Zn]=1 , Cov[Zi,Zj]=0
- 즉 기댓값은 n차원의 제로벡터, 공분산행렬은 n차원의 단위행렬 I가 됨
2. 일반적인 다변량 정규분포
1차원의 표준정규분포를 따르는 확률변수 Z~N(0,1)을 확대축소, 평행이동해서 여러 정규분포를 따르는 확률변수를 표현한 것 처럼
n차원의 표준정규분포를 따르는 확률변수 Z~N(o, I)를 변환해서 여러가지 변화를 나타낼 수 있음
확대 축소와 평행이동
원의 중심이 이동하고 기준 원의 반지름이 변화되나 모든 방향으로 균등하게 σ배가 되어 원의 모양이 바뀌진 않음
- 변환 : 확률변수 Z~N(o, I) → X ≡ σZ+µ
- 기댓값 : E[X] = σE[Z]+ µ = µ
- 분산 : V[X] = σ^2V[Z] = σ^2*I
종횡신축
축에 의해 늘어나고 줄어나는 배율을 바꿔 타원형의 분포를 만듦
- 변환 : 확률변수 Z~N(o, I) → X ≡ DZ+µ ~ N(µ, D^2)
- 기댓값 : E[X] = σE[Z]+ µ = µ
- 분산 : V[X]=D^2 , 대각성분이 σ1,σ2,..σn의 제곱인 대각행렬
- 변환 시, X ≡ (σ1,σ2,..σn)^T 으로 각 성분을 별개의 양의 정수로 변환
- X = DZ, D는 σ1,σ2,..σn이 대각 성분인 대각 행렬
회전
타원을 회전한 형태의 분포가 일반적인 다변량 정규분포
회전시키기 위해선 직교행렬을 곱해야 함
- 직교행렬 : 자기자신과 자기자신의 전치행렬을 곱했을때 단위행렬 I가 나오는 정사각 행렬 (QQ^T=Q^TQ=I)
- 직교행렬을 곱하는 방법
- 다변량 정규분포를 따르는 Z~N(o, I)에 임의의 대각행렬 D 곱해서 X ≡ DZ ~ N(o, D^2)로 변환
- Y = QX를 만듦 (Q는 직교행렬)
- E[Y] = Q*E[X] = Q*o = o
- V[Y] = V[QX] = Q^2*V[X]= Q*V[X]*Q^T = Q*D^2*Q^T
- 즉 일반적인 다변량 정규분포 Y ~ N(o ,V), (V=Q*D^2*Q^T)
- 여기에 상수벡터 µ를 더하면 원하는 위치로 중심을 이동시킬 수 있음
3. 다변량 정규분포의 확률밀도함수
- Z ~ N(o, I)를 따르는 확률변수일 경우
- 확률밀도함수 f_Z(z) = (1/√2π^n) * exp[(-1/2)*||z||^2]
- Y ~ N(o, V)를 따르는 확률변수일 경우 (V=Q*D^2*Q^T)
- 확률밀도함수 f_Y(y) = (1/(√2π^n * detV)) * exp[(-1/2)*y^T*V^-1*y ]
- 도출
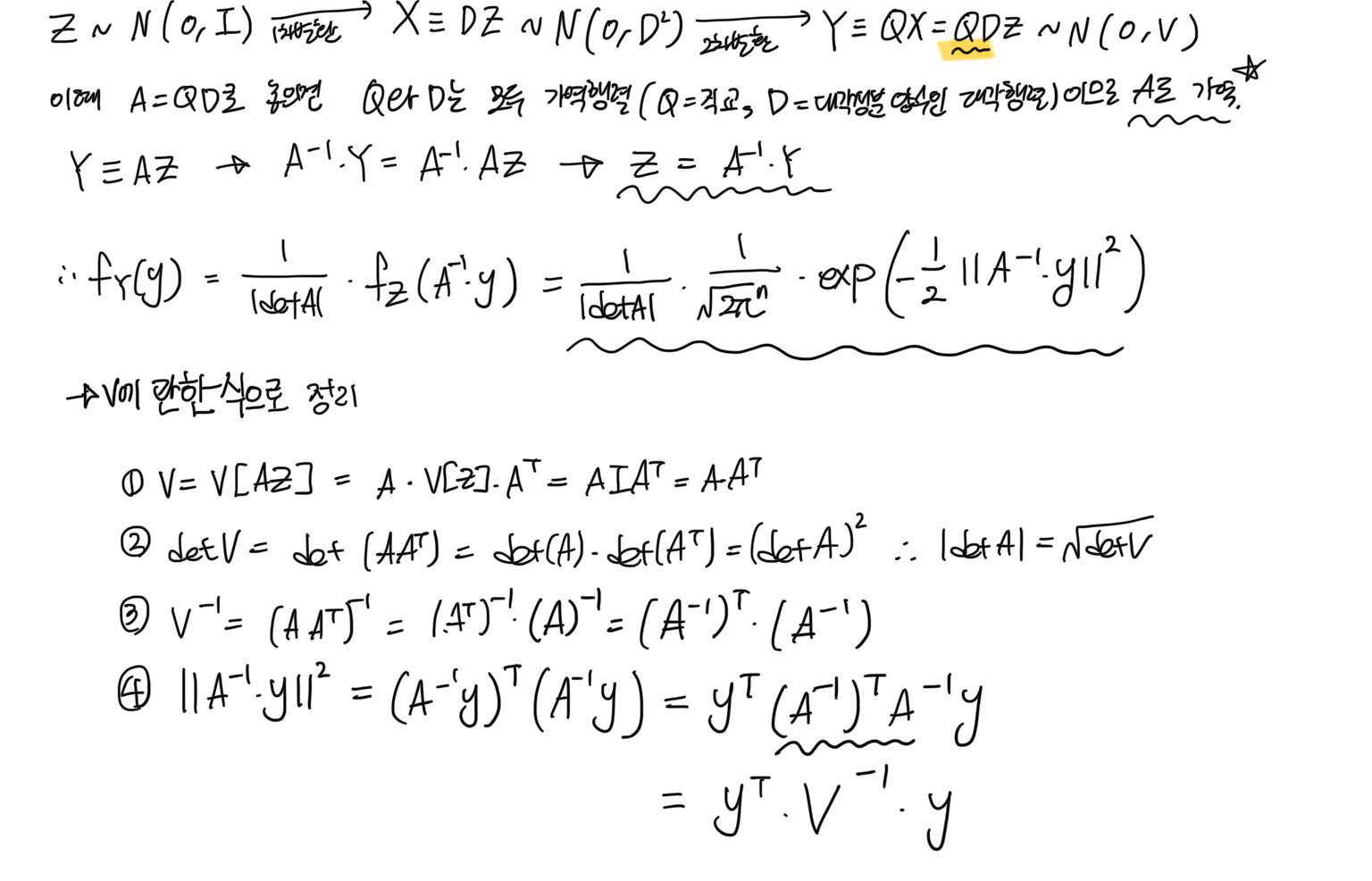
4. 다변량 정규분포의 성질
- 기댓값 벡터와 공분산행렬을 지정하면 분포가 정해진다
- 당연해서 패스
- 상관관계가 없는 것 만으로 독립적이라고 단언할 수 있다
- 일반적인 확률변수 X,Y에 대해 X,Y가 서로 독립이면 Cov[X,Y]=0이나, 이 반대는 반드시 성립하진 않았다.
- X ≡ (X,Y)^T가 2차원 정규분포라면 Cov[X,Y]=0이라면 바로 X,Y가 서로 독립이라고 말할 수 있음 (p.261)
- 간단하게 보면, Cov[X,Y]=0이면 이들의 공분산행렬은 대각행렬이며 그 역행렬도 대각임.
- 이들의 확률밀도함수는 x,y만의 수식으로 각각 분해될 수 있기 때문에 서로 독립임 (차원이 더 증가해도 마찬가지)
- 다변량 정규분포를 선형변환하면 다시 다변량 정규분포가 된다
5. 다변량 정규분포의 조건부분포와 주변분포
조건부분포(단면)
다변량 정규분포의 조건부분포는 다변량정규분포다
주변분포(그림자)
다변량 정규분포의 주변분포분포는 다변량정규분포다
'📝 CONCEPT > Statistics' 카테고리의 다른 글
| [Probabilistic Machine Learning 1] #4.2 MLE (0) | 2023.08.02 |
|---|---|
| #8. 공분산행렬 (0) | 2023.06.12 |
| #7. 실숫값에서 기대값, 분산,표준편차 구하기 (0) | 2023.06.12 |
| #6. 실수값에서의 변수 변환 (0) | 2023.06.05 |
| #5. 실수값을 위한 확률밀도함수 (0) | 2023.06.05 |