728x90
복습
- Score function : 카테고리 분류 시 선형식을 통해 score를 계산함으로 이미지의 카테고리를 도출함
- SVM Loss : SVM방식으로 해당 분류기의 성능을 확인하기 위해 오차를 계산함. SVM은 정답인 score가 safety margin을 두고 다른 score보다 높으면 되는 방식
- Regularization : Data Loss만으로는 train set에 과적합될 수 있기 때문에 가중치 W에 페널티를 줘서 단순하게 만드려는 정규화를 추가함. 이 때 정규화는 L1, L2가 있으며 해결하고자 하는 문제와 데이터에 맞는 방식을 선택하면됨
- 이를 바탕으로 Loss를 최소화하는 가중치 W를 찾고자 할때 경사하강법을 사용함
- 경사하강법 사용 시 수치적 gradient는 간단하지만 연산에 시간이 걸리므로 해석적 연산을 시행해야 함

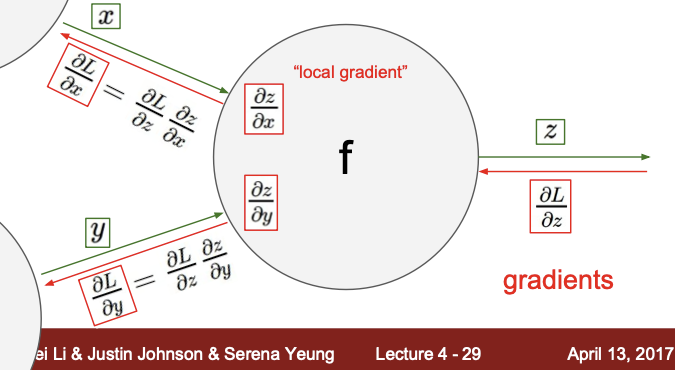
Backpropagation with Computational graph
- f : 연산
- x,y : 연산의 input
- z : 연산의 output
- local gradient : x-z, y-z처럼 foward propagation때 바로 구할 수 있는 gradient
- Global gradient : L-z처럼 뒤에서 앞으로 넘어올 때의 gradient
simple example
- 수행하는 연산 : +, *
- local gradient
- dq/dx, dq/dy, df/dq, df/dz 와 같이 forward시 수식으로 바로 연산 가능한 것들
- global gradient
- f 뒤에 더 많은 연산이 있었다고 가정했을 때, 그 결과값을 Loss라고 정의
- d Loss / dq와 같이 뒤에서 앞으로 역전파하는 것을 의미
- gradient = local gradient * global gradient
- chain rule : df/dy = df/dq * dq/dy
- 합성함수를 미분하는 것을 의미
- f(g(x))를 미분하면 f(g(x))' = f'(g(x)) * g'(x) 임을 이용하여 df/dx = df/dg*dg/dx
- 만약 d Loss / dx(gradient)를 구하고 싶다면
- dLoss/dq(global gradient) * dq/dx(local gradient) = (-4)*1 = -4
- chain rule : df/dy = df/dq * dq/dy

Another example
- 0) 맨 처음 global gradient = 1
- 1) 1/x
- 미분 시 -1/(x)**2
- local gradient : 1.37
- 미분 식의 x에 local gradient를 넣고 global gradient와 곱함
- -1/(1.37)**2 * 1 = -0.53
- 이를 매 노드마다 반복

- 시그모이드에 해당하는 부분을 묶고, 시그모이드에 대한 미분식으로 대체해도 동일한 결과가 나옴
- 시그모이드 미분 결과 : (1-sig(x))*sig(x)
- x에 local gradient 넣으면 0.2, global gradient는 1이므로 0.2

Patterns in backward flow
- add gate
- 직전의 gradient를 똑같이 분배해주는 역할
- max gate
- 둘 중에 큰 쪽으로 몰아줌
- mul gate
- 기존 gradient와 local gradient를 곱한 값을 두 노드 간 바꿔줌

Gradients for vectorized code
- x,y,z가 모두 벡터일 때 (실제 신경망에서의 상태, gradient는 벡터를 벡터로 미분한 것이 됨
- Jacobian matrix : 벡터를 벡터로 미분한 결과.
- 함수가 m개, 각 함수에 있는 변수가 n개 있을 때, 각 함수를 각 변수에 대해 미분하게 되면 m*n 행렬이 됨
- 이에 dz/dx를 하게 되면 x의 벡터 개수 * z의 벡터 개수 크기의 매트릭스를 도출할 수 있음
- Input의 각 요소는 Output의 해당 요소에만 영향을 줘서 대각 행렬이 됨


Vectorized operations
- gradient 계산 시, local gradient를 자코비안 행렬이 될 수 있음
- 이 때 Output을 input에 대해서 미분한 것이므로, 각 벡터의수를 행렬로 가짐
- 만약 미니배치를 수행하게 되면 각 행렬에 미니배치수를 곱한 숫자의 행렬을 갖게 됨

A vectorized example
- L2노드: f = ||q||**2 (제곱한 후 합하는거)
- *노드 : q = W*x
- df/dq = 2q
- L2는 제곱한 값이므로 L2를 미분하게 되면 df/dq = 2q, 이를 local gate인 [[0.22],[0.26]]과 곱함
- dq/dw = x
- df/dw = df/dq * dq/dw = 2q*x 인데 행렬간 연산이므로 x에 전치를 취해야함 즉 2q*x_t
- df/dx = df/dw와 동일하며 w,x만 바꾸면 되어 2q*w_t
- *은 곱셈이므로, mul gate처럼 global gradient인 [[0.44],[0.52]]를 각 다른 노드와 곱한 값 (전치행렬)

Modularized implementation: forward / backward API
- foward, backward를 객체지향으로 메서드로 각각 구현
- forward : 순전파 시 각 결과를 변수에 저장해야함 (나중에 사용함)
- backward : chain rule을 사용해서 오차 함수의 gradient를 계산
Neural Networks
- 함수를 계속 겹쳐나가며 레이어를 쌓아나가는 것
- (1) f = W1x : 선형함수
- - score를 구할 때 사용했었음
- - CIPAR의 예시로 x는 3072*1
- - W1 : 10*3072
- - f : 10*1 (class)
- (2) f= W2 * max(0,W1x)
- - max : 음수인 값을 0으로, 다른 값은 그대로 전달
- - x : 3072 * 1
- - W1 : 100* 3072
- - W2 : 10*100
- (3) f = W3 * max(0,W2*max(0,W1x))
- - 3 layer 신경망
- (1) f = W1x : 선형함수

- 신경망은 인간 뉴런 구조와 러프하게 유사함

class Neuron :
def neuron_tick(inputs):
cell_body_sum = np.sum(inputs * self.weights) + self.bias
firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)
return firing rate- 활성함수 예시들

- FC layer example
- Dense layer(fc)는 아래처럼 모든 노드가 연결됨
#활성함수
f = lambda x : 1.0/(1.0 + np.exp(-x))
#input, W는 이미 있다고 가정
x = np.random.randn(3,1)
#layer
h1 = f(np.dot(W1,x) + b1)
h2 = f(np.dot(W2,h1) + b2)
out = np.dot(W3,h2) + b3

'👩💻LEARN : ML&Data > Lecture' 카테고리의 다른 글
| [CS231n] Lecture6. Training Neural Networks 1 (0) | 2023.05.14 |
|---|---|
| [CS231n] Lecture5. Convolutional Neural Networks (0) | 2023.05.14 |
| [CS231n] Lecture3. Loss Functions and Optimization (1) | 2023.05.10 |
| [CS231n] Lecture2. Image Classification Pipeline (0) | 2023.05.08 |
| [알고리즘 구현으로 배우는 선형대수] #11. 직교 행렬 (0) | 2023.04.13 |