
#7. Gradient descent for logistic regression
로지스틱 회귀에서 cost function 수식까지 구해봤는데, 이를 최소화할 수 있는 경사하강법은 어떻게 수행할 수 있을까
Cost function을 줄이기 위해 기존에 배웠던 경사하강법 처럼 아래 내용을 반복하며 파라미터를 업데이트해나갈 수 있음
- wj = wj - alpha * (dj/dw)
- b = b - alpha * (dj/db)
그런데 여기서 문제는, j의 수식이 cost function for logistic regression으로 바뀌었다는 것임. 이때의 기울기는 어떻게 구할 수 있을 지 살펴봐야 함
- ... 사실 똑같음. f(x)가 다르기 때문에 기존 선형회귀때 기울기 구했던 것과 똑같이 수행하면 됨.

#로지스틱회귀에 경사하강법 적영해보기
def compute_gradient_logistic(X, y, w, b):
"""
Computes the gradient for linear regression
Args:
X (ndarray (m,n): Data, m examples with n features
y (ndarray (m,)): target values
w (ndarray (n,)): model parameters
b (scalar) : model parameter
Returns
dj_dw (ndarray (n,)): The gradient of the cost w.r.t. the parameters w.
dj_db (scalar) : The gradient of the cost w.r.t. the parameter b.
"""
m,n = X.shape
dj_dw = np.zeros((n,)) #(n,)
dj_db = 0.
for i in range(m):
f_wb_i = sigmoid(np.dot(X[i],w) + b) #(n,)(n,)=scalar. sigmoid 씌우기
err_i = f_wb_i - y[i] #scalar #오차 세팅해주기
for j in range(n): #w수 만큼 dj_dw 업데이트+합해주기
dj_dw[j] = dj_dw[j] + err_i * X[i,j] #scalar
dj_db = dj_db + err_i #전체 수 만큼 dj_db 합해주기
dj_dw = dj_dw/m #(n,)
dj_db = dj_db/m #scalar
return dj_db, dj_dw쉽게 사이킷런으로 돌려보기
#불러오기
from sklearn.linear_model import LogisticRegression
#모델세팅해주기
lr_model = LogisticRegression()
lr_model.fit(X, y)
#예측해주기
y_pred = lr_model.predict(X)
print("Prediction on training set:", y_pred)
#8. The problem of overfitting
The problem of overfitting
- Underfit : 예측선이 데이터를 잘 설명하지못하는 경우 (=high bias)
- 좋은 모델 : 적당히 training 데이터의 경향성을 설명한 경우 (=Generalization)
- Overfit : 예측선이 정확하게 training 데이터를 설명했지만, 실 데이터는 설명하지 못한 경우 (=high variance)
Classification에 적용한 경우
: z를 어떤 수식으로 세팅하느냐(어떤 파라미터를 세팅하느냐)에 따라 underfit - overfit 될 수 있음
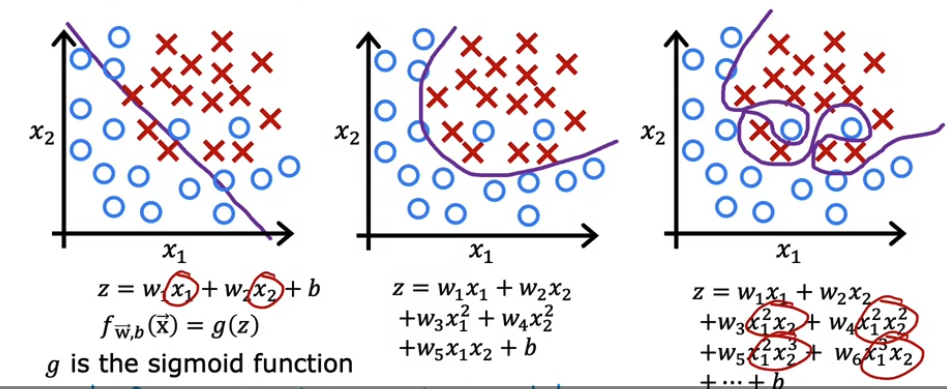
Addressing overfitting
오버피팅에 어떻게 대응할 것인가!
Collect more training examples
- 하지만...항상 가능하진 않다
Select features to include/exclude
- 여러 featrure들을 가지고 있는데 데이터 수가 부족한 경우에도 오버핏이 발생함
- y를 잘 설명할 것으로 보이는 feature들을 선택해서 트레이닝하자
- 하지만 중요한 feature를 놓칠수도 있음
Regularization ⭐️
- parameter w 의 사이즈를 줄이자..! (e.g. 150 -> 0.01로 줄이는 등)
- b의 사이즈를 줄이는건 큰 영향을 미치진 않음
Cost function with regularization
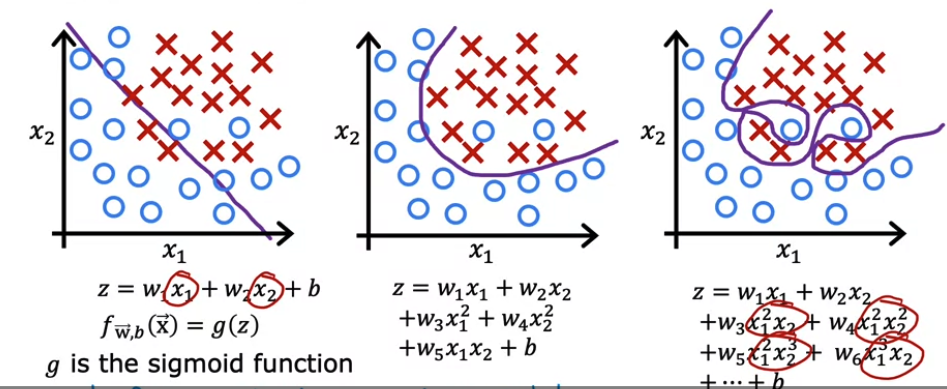
위 그림의 맨 우측 그림처럼 오버피팅된 모델이 있을 때, cost를 최소화하기 위해 cost function을 사용
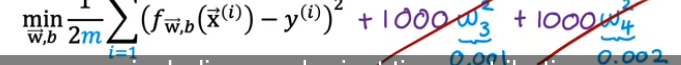
by x**3, x**4에 매우매우 큰 수(=w)를 곱하고 비용함수에 더해줌
→ 경사하강법 입장에서는 cost를 최소화하기 위해 x3,x4를 0에 가깝게 만들 수 밖에 없음
→ w3,w4는 사실상 0에 수렴하게 되어 2차 방정식이 됨
→ 즉 일부 파라미터를 매우 작은값으로 만들어 방정식의 차수를 축소시켜서 심플한 방정식을 만드는 정규화를 진행
→ 오버핏 확률이 줄어듦
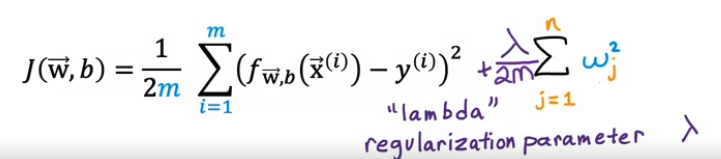
즉 기존 비용함수에 람다를 곱한 w의 제곱합들을 더해 f(x)를 단순하게 만들어주려는 것
※람다
- 정규화 parameter
- > 0, 학습률처럼 람다의 설정값에 따라 성능이 좌우됨. 그러므로 mean squared error (데이터에 fit하게 만드려는 목적)와 reguralization term(wj를 작게 만드려는 목적) 을 밸런싱을 잘 할 수 있는 람다 값을 설정하는 것이 중요
- b에 적용하는 것도 가능하나 학습의 입장에서는 w에서만 적용하는 것으로 배우겠음
Regularized linear regression
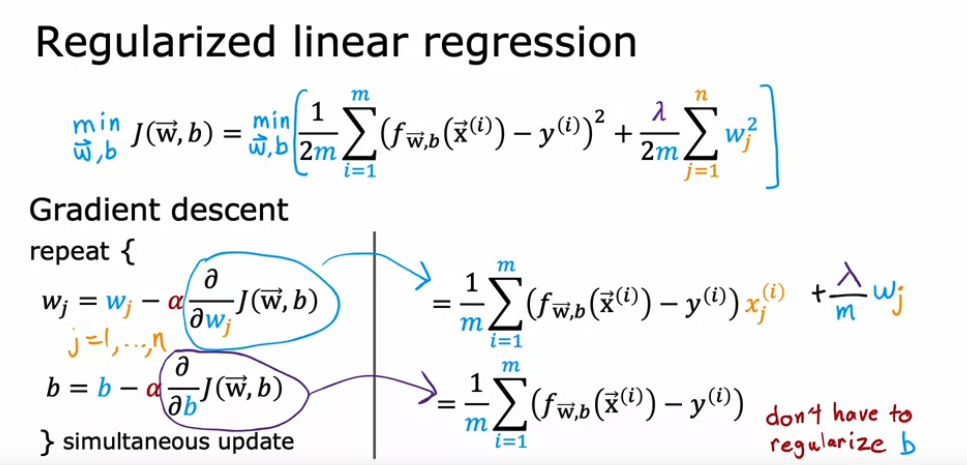
- 기존에 있던 Cost function을 regularize하기 위해 regularized parameter 를 추가함
- 경사하강법에 따라 wj, b는 dj를 각각 dw, db로 미분한 기울기를 이전 w값에서 빼면서 값을 업데이트 해왔음
- regularized parameter가 추가 됨에 따라 wj의 기울기 구하는 수식이 달라짐 (b는 정규화하지 않으므로 패스)
이를 코드로 구현하려면 다음과 같음

wj에 대해서만 더 디테일하게 보면 아래와 같이 기존 경사하강법에 새로운 정규화 파트가 더해진걸 볼 수 있음
→ 람다가 1이되면 wj는 1에 가까운 수 (0.998등) 이 되어 업데이트 될 때 기존 wj보다 약간 작아진 상태로 업데이트됨 (=정규화실행!. 람다가 0 이면 정규화 ㄴㄴ )

Linear regression에서의 cost 값 구하기
def compute_cost_linear_reg(X, y, w, b, lambda_ = 1):
"""
Computes the cost over all examples
Args:
X (ndarray (m,n): Data, m examples with n features
y (ndarray (m,)): target values
w (ndarray (n,)): model parameters
b (scalar) : model parameter
lambda_ (scalar): Controls amount of regularization
Returns:
total_cost (scalar): cost
"""
m = X.shape[0]
n = len(w)
cost = 0.
for i in range(m):
f_wb_i = np.dot(X[i], w) + b #(n,)(n,)=scalar, see np.dot
cost = cost + (f_wb_i - y[i])**2 #scalar
cost = cost / (2 * m) #scalar
reg_cost = 0
for j in range(n):
reg_cost += (w[j]**2) #scalar
reg_cost = (lambda_/(2*m)) * reg_cost #scalar
total_cost = cost + reg_cost #scalar
return total_cost #scalarLinear regression에서 경사하강법 해보기
def compute_gradient_linear_reg(X, y, w, b, lambda_):
"""
Computes the gradient for linear regression
Args:
X (ndarray (m,n): Data, m examples with n features
y (ndarray (m,)): target values
w (ndarray (n,)): model parameters
b (scalar) : model parameter
lambda_ (scalar): Controls amount of regularization
Returns:
dj_dw (ndarray (n,)): The gradient of the cost w.r.t. the parameters w.
dj_db (scalar): The gradient of the cost w.r.t. the parameter b.
"""
m,n = X.shape #(number of examples, number of features)
dj_dw = np.zeros((n,))
dj_db = 0.
for i in range(m):
err = (np.dot(X[i], w) + b) - y[i]
for j in range(n):
dj_dw[j] = dj_dw[j] + err * X[i, j]
dj_db = dj_db + err
dj_dw = dj_dw / m
dj_db = dj_db / m
for j in range(n):
dj_dw[j] = dj_dw[j] + (lambda_/m) * w[j]
return dj_db, dj_dw
Regularized logistic regression
로지스틱 회귀에서 정규화 시키는 것 역시 상당히 비슷함
1. Cost function
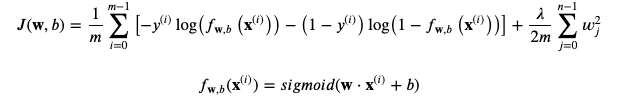
2. Gradient Descent
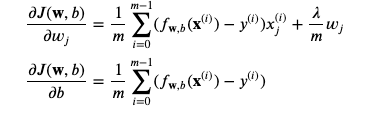
로지스틱 회귀를 위한 Cost 구하기
def compute_cost_logistic_reg(X, y, w, b, lambda_ = 1):
"""
Computes the cost over all examples
Args:
Args:
X (ndarray (m,n): Data, m examples with n features
y (ndarray (m,)): target values
w (ndarray (n,)): model parameters
b (scalar) : model parameter
lambda_ (scalar): Controls amount of regularization
Returns:
total_cost (scalar): cost
"""
m,n = X.shape
cost = 0.
for i in range(m):
z_i = np.dot(X[i], w) + b #(n,)(n,)=scalar, see np.dot
f_wb_i = sigmoid(z_i) #scalar
cost += -y[i]*np.log(f_wb_i) - (1-y[i])*np.log(1-f_wb_i) #scalar
cost = cost/m #scalar
reg_cost = 0
for j in range(n):
reg_cost += (w[j]**2) #scalar
reg_cost = (lambda_/(2*m)) * reg_cost #scalar
total_cost = cost + reg_cost #scalar
return total_cost #scalar경사하강법(사실상 동일)
def compute_gradient_logistic_reg(X, y, w, b, lambda_):
"""
Computes the gradient for linear regression
Args:
X (ndarray (m,n): Data, m examples with n features
y (ndarray (m,)): target values
w (ndarray (n,)): model parameters
b (scalar) : model parameter
lambda_ (scalar): Controls amount of regularization
Returns
dj_dw (ndarray Shape (n,)): The gradient of the cost w.r.t. the parameters w.
dj_db (scalar) : The gradient of the cost w.r.t. the parameter b.
"""
m,n = X.shape
dj_dw = np.zeros((n,)) #(n,)
dj_db = 0.0 #scalar
for i in range(m):
f_wb_i = sigmoid(np.dot(X[i],w) + b) #(n,)(n,)=scalar
err_i = f_wb_i - y[i] #scalar
for j in range(n):
dj_dw[j] = dj_dw[j] + err_i * X[i,j] #scalar
dj_db = dj_db + err_i
dj_dw = dj_dw/m #(n,)
dj_db = dj_db/m #scalar
for j in range(n):
dj_dw[j] = dj_dw[j] + (lambda_/m) * w[j]
return dj_db, dj_dw
Summary

https://coursera.org/share/06dfd5a477e0de26a02de2eb4fb851ae
Completion Certificate for Supervised Machine Learning: Regression and Classification
This certificate verifies my successful completion of DeepLearning.AI's "Supervised Machine Learning: Regression and Classification " on Coursera
www.coursera.org
3일간의 노력 끝에 우선 첫번째 수료증 취득 완료..!