
퍼셉트론의 한계, 은닉층에 있는 가중치를 자체적으로 학습하는 방법이 없었으나 이를 해결한 것이 제프리 힌튼의 오차역전파이다.
간단하게 정리해보자면, 한번 x 입력층에서 y 출력층까지 순서대로 계산해 각 가중치의 초기값을 확인한 다음, 이 초기값의 값과 실제값을 비교하며 오차를 수정해나가는 과정이다. 그 과정에서 은닉층에 있는 가중치들을 y 출력층의 최종값으로부터 역계산(오차공식+편미분)해나가야 한다.
이 때 활성화 함수로 사용된 시그모이드 함수를 계속 미분하게 되면 0.**이 나와 계속 곱하다보면 0에 수렴하는 문제점이 있어 이를 해결하기 위해 ReLu함수를 사용한다.
이렇게 정리해놓으면 개념적으론 이해가 되었는데, 이 과정에서의 수식들이...꽤나 골치가 아프다...
비록 이 책이 매우매우 친절한 편이지만 나는 아직 미분을 배운 지 한달이 채 안된 응애이기 때문에
응애도 찰떡같이 이해할 수 있는 자료가 필요했고.... 검색하다 보니 아래와 같은 유튜브 채널이 있어 이를 바탕으로 다시 오차역전파를 정리해보려고 한다
https://www.youtube.com/watch?v=kDZ3QB3_uR4&list=PLsS-TVNjbU7clDOjpAZKud3uG8APHDq_M&index=83
#2-8. 오차역전파 (feat. 유튜브)
1. 오차역전파 개요
- 목적 : 가중치와 바이어스를 미리 알아보고 넣는 것이 아니라, 데이터를 통해 스스로 가중치를 조절하는 학습을 실현시키는 것
- 방법 : 경사하강법의 활용 ( 임의의 가중치 선언 → 결과값 활용한 오차 확인 → 오차가 최소인 지점으로 이동 )
- 한계 : 은닉층이 생기며 두번 이상의 경사하강법을 사용하며 가중치를 두번 수정해야 함 → 하면됨 ㅇㅇ

... 역으로 뭔가 계산하면 된다는건 알겠지만 그 과정에서 사용했던 평균제곱오차공식과 편미분 공식 등이 쉽게 떠오르진 않는다.
유튜브에 도움을 받아보자
🖥 유튜브 처음코딩 [바로가기]Sample 예시의 계산 그래프  - 역전파라는 것은 결국 빨간 값을 구해나가는 것 (사과의 값이 변하면 장바구니에 담은 값은 어떻게 변화하는가) 합성함수와 연쇄법칙  - 합성함수 그 자체를 미분하는 것은 어렵기 때문에 이를 합성함수의 각 구성으로 나누어 각각 미분한 후 곱한다  - 위의 역전파에 연쇄법칙을 적용해보면, - 최종 결과값이 z일 때에 - (1)z를 z에 대해 미분 (자기자신에 대한 미분이기 때문에 값은 1) - (2)z를 t에 대해 미분한 다음 (1)을 곱함 (여기서 z = t**2) - (3) t를 x에 대해 미분한 다음 (1)(2)를 곱함 (여기서 t = x+y) - 최종값은 1 * 2t * 1 = 1 * 2(x+y) * 1 = 2(x+y) 가 됨 결국 미분한 값들은 해당 단계에 있는 값들이 최종계산값에 어떤 영향을 미치는 지 알 수 있게 해준다 If 덧셈노드일 경우 : 이전 단계에서 온 값이 그대로 전달 (왜냐면 덧셈을 미분하면 1밖에 안나옴)  If 곱셈노드일 경우 : 미분하는 것에 곱해진 값을 이전 단계에서 온 값에 곱함 - z= x*y일 경우, x에 대해 미분하면 y가 남음  🥲 여기까지 보면 참 쉬운데... |
찾다보니 모두의 딥러닝 원저자의 유튜브 강의도 있었다. 책으로 이해하기 힘든 영역은 영상 보면서 확인하면 바로 이해가 된다.
https://www.youtube.com/watch?v=573EZkzfnZ0
개념적으론 절대 어려운게 아니다. 이제 공식을 보면서 은닉층에서 오차를 어떻게 고쳐나가는지 확인해보자
2. [심화] 오차 역전파 계산
[오차 업데이트 공식]
현재단계의 가중치 w(31)은 이전단계의 가중치w(31)에서 최종 결과값(Yout)을 w(31)로 편미분한 값을 뺀 것이다.
🤩 여기서 가장 걸림돌이 되었던 거는 왜 그 값을 빼느냐! 였는데
인터넷을 찾다 찾다 그 이유를 다른 분이 정리해준 곳에서 알게되었다 (야호! 감사합니다!)
오차 역전파의 방식
1. 임의의 초기 가중치를 둔 이후 결과를 계산한다 (Yout)
2. 계산 결과와 실제 값 간의 차이인 오차를 계산한다.
3. 경사하강법을 활용해 오차가 작아지는 방향으로 가중치를 업데이트 한다 (기울기, 즉 미분값이 0 에 가까워지는 방향으로)
4. 이를 오차가 더 이상 줄어들지 않을 때 까지 반복한다
✔ 기울기, 즉 미분값이 0에 가까워지면 가중치에서 기울기를 빼도 가중치가 변하지 않는다 (사실상 0을 뺀 모양새)
✔ 즉 오차 역전파 = 가중치에서 기울기를 빼도 값의 변화가 없을 때까지 계속해서 가중치 수정 작업을 반복하는 것
→ W(t+1)=W * t − ∂오차/∂W
새로운 가중치(W(t+1))는 현재 가중치(W)에서 기울기(∂오차/∂W)를 뺀 값
😇 여기에서 왜 기울기는 오차를 가중치로 편미분한 값인가?
- 가중치가 미세하게 움직였을 때 오차가 이에 영향을 받음. 우리는 오차를 최소화 하는 것이 목적이므로 오차를 최소화 시키는 가중치로 오차를 편미분하는 것이 적합함
오차 업데이트 공식을 알았으니, 이 공식에서 계산해야 하는 ∂오차/∂W 를 구해보자
[오차 공식 : 먼저 오차를 구하자 ]
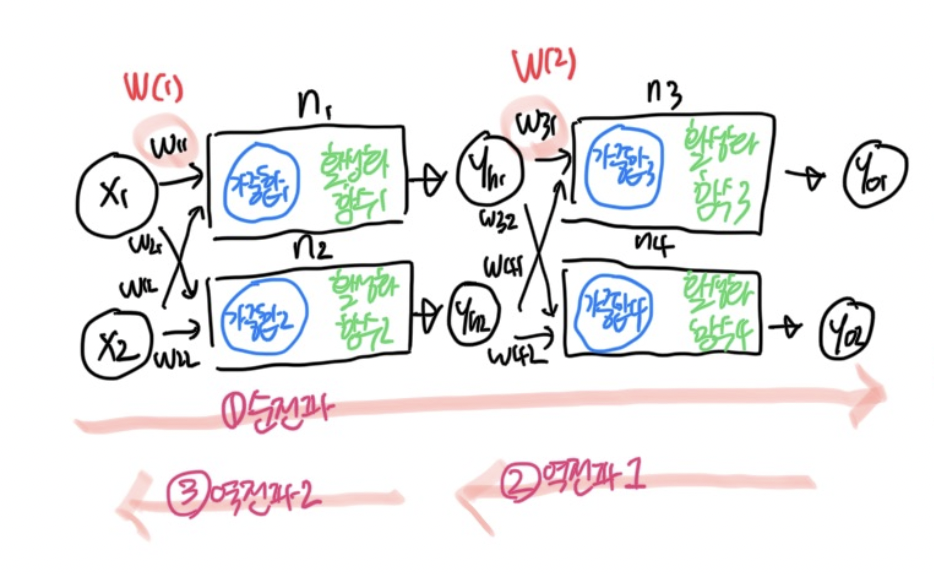
오차 Y(out)은 y(out1)과 y(out2)로 구성되어 있으므로 이를 각각 구해야 한다. 이 때 오차를 구하는 방식은 평균 제곱 오차를 활용한다.
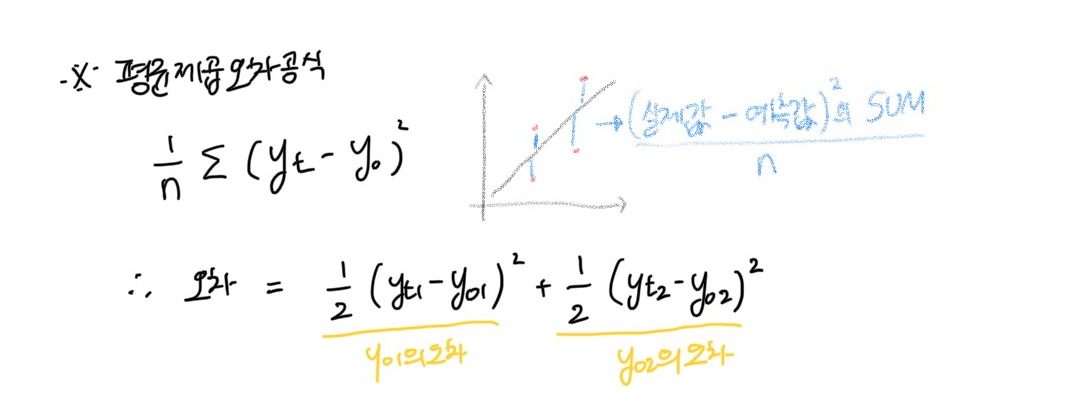
[오차를 가중치로 편미분해주자 w/체인룰 ]

이렇게 구한 값을
오차 업데이트에 사용하여 새로운 가중치를 구할 수 있음.
즉 출력층의 가중치를 업데이트하는 방법은 아래와 같음
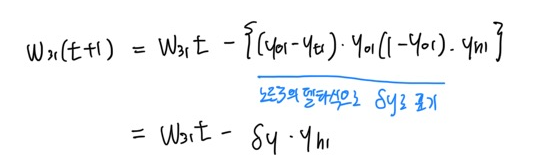
이젠...은닉층의 가중치 업데이트가 남아있다....
그래도 앞에 거 이해했으니까 어찌저찌 될거야 와타시 화이팅!
'👩💻LEARN : ML&Data > Book Study' 카테고리의 다른 글
| [모두의 딥러닝] #4-10. 딥러닝 모델 설계하기 (0) | 2023.02.15 |
|---|---|
| [모두의 딥러닝] #3-8. 오차역전파 : 은닉층 오차 수정과 계산 (0) | 2023.02.14 |
| [모두의 딥러닝] #2-7. 퍼셉트론 (0) | 2023.02.12 |
| [모두의 딥러닝] #2-6. 로지스틱 회귀 모델 (0) | 2023.02.11 |
| [모두의 딥러닝] #2-5. 선형회귀모델 : 먼저 긋고 수정하기 (0) | 2023.02.10 |